삼각 함수 & 구면좌표계-01

삼각 함수  :

 

 

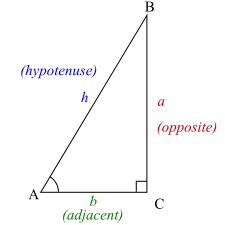
삼각함수 항등식 :

 

                   

                 

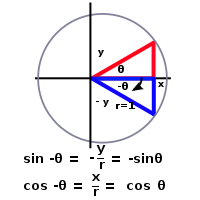
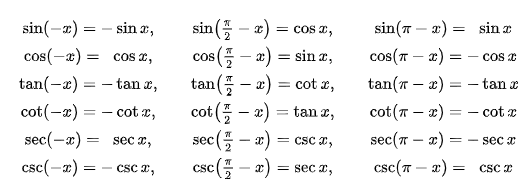
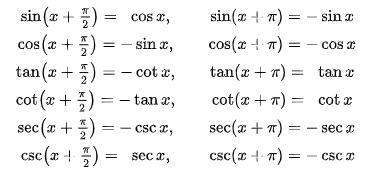
2019/09/02 - [C++(Math&알고리즘)] - Rotation Matrix

Rotation Matrix

                 

구면 좌표계 :

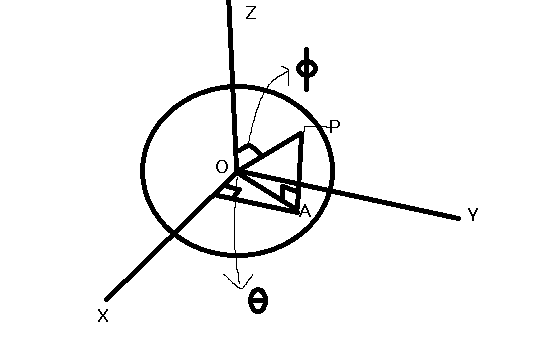
그림을 보시면서 천천히 따라 가시면 될것 같습니다 .

먼저 OA 직선을 구하려고 할떄 OP의 직선과 파이를 알고 있다면 

$$OA=OP*\cos(\pi/2-\phi)$$

여기서 삼각함수 항등식에 의하면 

$$OA=OP*\sin(\phi)$$

다음은 P의 좌표인 (x,y,z)를 구해보겠습니다.

$$x=OA*\cos(\theta)$$

왜냐하면 삼각형을 떼서 보면

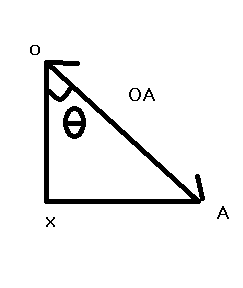
위의 그림과 같다. 그렇다면 코사인세타는

 

$$OX/OA=\cos(\theta)$$

 

이다

 

그래서

$$x=OA*\cos(\theta)$$

$$OX/OA=\cos(\theta)$$

$$OA*OX/OA$$

입니다.

그러면 

$$OX$$

가 남습니다.

즉  x좌표는 

 

$$x=OA*\cos(\theta)$$

 

입니다.

그렇다면

위에서 OA 값은

 

$$OA=OP*\sin(\phi)$$

 

였습니다. 

그걸 변경을 하면 

 

$$x=OA*\cos(\theta)$$

$$x=OP*\sin(\phi)\cos(\theta)$$

 

이런식으로 변경이 됩니다. 

 

다른 좌표들도 마찬가지로 

정리해보면 

x좌표 

$$x=OA*\cos(\theta)$$

$$x=OP*\sin(\phi)\cos(\theta)$$

y좌표는 

$$y=OA*\cos(\pi/2-\theta)$$

$$y=OP*\sin(\phi)*cos(\pi/2-\theta)$$

$$y=OP*\sin(\phi)\sin(\theta)$$

 z 좌표는 

$$z=OP*\sin(\pi/2-\phi)$$

$$z=OP*\cos(\phi)$$

이다.

그렇다면 구의

$$x^2+y^2+z^2=OP^2$$

를 증명하자면 

위에 구한 좌표값을 전부 넣어보니다.

$$x^2+y^2+z^2=OP^2$$

$$x^2+y^2+z^2=(OP*\sin(\phi)\cos(\theta))^2+$$

$$(OP*\sin(\phi)\sin(\theta))^2+(OP*\cos(\phi))^2$$

식을 풀면 

$$(OP^2*\sin(\phi)^2*(\cos(\theta)^2+\sin(\theta)^2)$$

$$+OP^2\cos(\phi))^2$$

$$\cos(\theta)^2+\sin(\theta)^2=1$$

그러므로

$$OP^2*\sin(\phi)^2*1+OP^2\cos(\phi))^2$$

가 됩니다. 

정리하면

$$OP^2*\sin(\phi)^2+OP^2\cos(\phi)^2$$

다시한번 

$$OP^2$$

으로 묶으면

$$OP^2*(\sin(\phi)^2+cos(\phi)^2)$$

됩니다.

그러면 마찬가지로 1이 되므로 

$$OP^2*1$$입니다. 

즉

$$x^2+y^2+z^2=OP^2$$

입니다.

 

그렇다면 각도의 값들은 어떻게 구할까요 

위의 그림의 각도인

$$\theta , \phi$$

구해보겠습니다.

$$\phi=\arccos(z/OP)$$

$$\theta=\arctan(y/x)$$

인데 이를 증명해보이겠습니다.

먼저 

$$z=OP*\cos(\phi)$$

이용하여  구해보겠습니다.

$$z/OP=cos(\phi)$$

$$\arccos(x)=cos (y)$$

$$\phi=acrccos(z/OP)$$

다음에는 

$$\tan \theta=(y/x)$$

$$\arctan (x) =\tan (y)$$

$$\theta=\arctan (y/x)$$

이다