OBB(Object Oriented Bounding Box) Collision

OBB충돌을 이해하기 위해서 조금 시간이 걸리긴 했지만 외국 사이트 내용이 생각보다 쉽지 않아서 국내 블로그를 전전하다가 굉장히 설명이 잘되있는곳을 알게 되었습니다.
링크:http://www.gingaminga.com/Data/Note/oriented_bounding_boxes/

Object Oriented Bounding Box 를 이용한 Collision Detection

솔직히 다른곳은 설명을 봐도 잘모르겠더라고요 
여기 링크된곳이 가장 설명이 좋은것 같습니다. 혹시나 다른곳이 있으면 링크라도 남겨주세요
저는 위 링크 블로그를 참조하여 좀더 보기좋게 직관적으로 설명을 드리려고합니다.
 

예를들어 박스의 충돌이 일어날때 AABB충돌은 면과 면의 충돌이지만 여기서 보이는 A박스와 B박스는 A박스가 기울어진 상태로 부딫치면 면과면이 아닌 모서리가 먼저 닿게 됩니다.
그래서 박스가 좀더 커진 상태로 충돌이 될 위험성이 있습니다. 이를 방지하기 위해 만들어진 obb 충돌이 있습니다.
그렇다면 어떤걸 이용해서 충돌이 일어나는지에 대해서 알아야합니다.
 

이런식으로 A박스가 움직이는 박스이고 B가 이제 멈춰있는 박스라고 가정을 해보겠습니다.
 

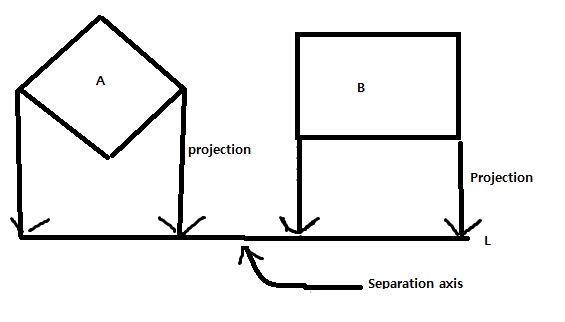
이부분은 제가 글을 보면서 이해하는 부분이어서 확실치는 않습니다 만약 틀리면 조금더 수정을 하도록하겠습니다.
Separation axis는 가상의 선으로서 마치 저희가 보는 실제하는 차원이 3차원이라는 공간의 영역입니다. 
그렇다면 사진을 찍으면 저희는 2차원이라는 면의 영역으로 나타납니다. 이를 저는 projection이라고 이해했습니다.
즉 Separation axis는 카메라의 역할을 하는 부분이라고 생각하면될것 같습니다.
 
그렇다면 저희는 A박스와 B박스를 separation axis로 projection(투영)을 합니다. separation axis를 L이라는 벡터라고 가정하겠습니다. 투영할때는 가장 긴 가장자리로 합니다.
 

위의 그림처러 이제 빨간 부분이 바로 projection(투영) 된 A와 B입니다.
이 projection(투영)을 시킨 영역을 이용해서 저희는 충돌이 되었는지 안되었는지를 감지합니다.
 
그림을보시면 

조금 헷갈릴수도 있습니다 하나씩 설명드리겠습니다.  A중점와  B  중점의 거리는 T라고 하겠습니다 
마찬가지로 T 또한 projection이 가능합니다.  그리고 저희는 이 T는 방향성을 가진 벡터입니다. 
즉 A에서 B로 가는 방향성을 가진 벡터라고 가정을 하면 저희는 이걸 스칼라로 바꾸기 위해서 L과
T의 내적을 구합니다. 그렇다면 즉 충돌의 범위가 나오게됩니다.(이부분은 벡터의 내적에 대해서 이해하셔야합니다.)
 
그다음 저희는 ra(노란범위)라는 projection된 범위와 rb(노란범위)라는 projection된 범위가 T ,L 내적보다 작으면 충돌이 발생하지 않고 있다는 뜻입니다 반대로 T,L내적보다 ra,rb (노란범위)합이 더 크면 충돌이 발생했다는 뜻입니다.
수식으로 나타내면 -> T·L >ra+rb (충돌 아님)
                            T·L <=ra+rb (충돌)
T L은 내적이기에 스칼라이면 ra,rb또한 스칼라입니다. 그렇다면 ra, rb는 어떻게 구하는지 알아보도록 하겠습니다.
기억하셔야합니다. 벡터의 내적은 벡터가 아니라 스칼라입니다.
 
ra, rb 이번에 어떻게 구해야하는지 알아보겠습니다. 
 

 
먼저 벡터의 합과 곱을 알아보도록 하겠습니다. 벡터는 합은 벡터 그대로 나오며 벡터의 내적은 스칼라는 사실을 알고 가야합니다. 위의 그림을 참고하시면 같은 90도의 벡터를 계산을 해도 합과 내적은 다른계산이 된다는 사실을 잊으면 안됩니다.
ra는 먼저 
 

그림을 보시면 a1 과 a2의 벡터의 합입니다. 그리고 아래 그림의 분리축인 L에게 내적을 한 값이
 

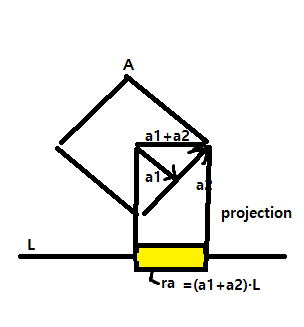
그리고 위 그림의 분리축벡터 L과 벡터 (a1+a2)의 내적을 한 값 ra입니다.
rb도 같은 방법으로 계산을 하면됩니다. 
나머지 방향으로도 마찬가지로 계산을 해주시면됩니다.